• 题解

  • 2022第五届西南石油大学程序设计新生赛题解

  • @ 2022-12-1 20:22:37

A.联合招新

考点：输出语法

定位：究极签到

题意：

就直接输出给出的那几个字符就行没少好说的过了

B.一个简单的伪并行程序

考点：循环，数组

定位：l1语法签到

题意：

大概就是说给你n个数，m个核，然后你需要先把这n个数相邻加和变成m个核，然后再每两个核加和变成一个新的核，以此类推直到只剩一个数，这个题很简单读完题就知道怎么做不读题看样例都能猜出来

代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,N;
int S[1000000];
void threa(int S[]){
	int last;
	int divisor = 2, core_difference = 1;
	for (;divisor <= m;){
		for (int first = 0; first < m; first += divisor){
			last = core_difference + first;
			S[first] += S[last];
			cout<<S[first];
			if(first+divisor<m) cout<<" ";
		}
	 divisor *= 2, core_difference *= 2;
	 if(divisor<=m) cout<<endl;
	}
}

int main(){
	cin>>n>>m;
	N=n/m;
	int c1=0,k=0;
	for(int c=0;c<n;c++){
		int a;
		cin>>a;
		S[k]+=a;
		c1++;
		if(c1==N){
			cout<<S[k];
			if(c!=n-1) cout<<" ";
			c1=0;
			k++;
		}
	}
	cout<<endl;
	threa(S);
}

C.摆火柴

考点：思维，构造

定位：l2带坑点的构造

这道题主要还是要处理好细节，按照题意一步一步来就没什么问题了。

首先我们要把从0~9这10个数字所需要的火柴通过数组来进行储存。

int a[N]={6,2,5,5,4,5,6,3,7,6};

并且我们需要10~1000这些数所需要的火柴，这就要把数拆分成一位一位的来进行火柴计算

for(int i=10;i<100000;i++){
    int p=i;
    while(p>9){
        int m=p%10;
        a[i]+=a[m];
        p/=10;
    }
    a[i]+=a[p];
}

然后我们就可以看到他是加号和等号也是需要火柴的（这里就直接记上，”+“需要2根，“=”也是需要两根，这里特别注意还有“==”这是需要4根火柴的），这里A+B=C,与B+A=C是不同的两个等式，那么我们就要注意当A与B不一样的时候，我们就要交换AB的位置，就又可以成为一个新的等式，所以直接乘2。

这里tt是表示所拥有的火柴中减去ABC还有+号和一个”=“所剩下的火柴，这里就要对”=“和”“来进行特别处理，如果还剩2个以上，那么就可以用”“表示来那么我们就直接加2种方案，如果A和B不同那我们再加2种方案。如果剩下的不足摆出”==“那我们就只有加’=‘的一种方案。

if(tt>=2) {
    *//cout<<i<<"+"<<j<<"=="<<i+j<<endl;*
        if(i!=j) ans+=2;
    ans+=2;
}else if(tt>=0){ 
    *//cout<<i<<"+"<<j<<"="<<i+j<<endl;*
        if(i!=j) ans++;
    ans++;
}  if(tt>=2) {
    *//cout<<i<<"+"<<j<<"=="<<i+j<<endl;*
        if(i!=j) ans+=2;
    ans+=2;
}else if(tt>=0){ 
    *//cout<<i<<"+"<<j<<"="<<i+j<<endl;*
        if(i!=j) ans++;
    ans++;
}

因为A和B都是到1000所以可以直接循环来找。

代码：

#include<iostream>
#include<cstdio>
#include<string.h>
#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
#include<stack>
#include<queue>
#define lowbits(x) ((-x)&x)
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 1e5+5;
typedef long long ll;
int gcd(int a,int b)
{
    return b>0 ? gcd(b,a%b):a;
}
int a[N]={6,2,5,5,4,5,6,3,7,6};
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int n,ans=0;
    cin>>n;
    for(int i=10;i<100000;i++){
        int p=i;
        while(p>9){
            int m=p%10;
            a[i]+=a[m];
            p/=10;
        }
        a[i]+=a[p];
    }
    for(int i=0;i<1000;i++){
        for(int j=i;j<1000;j++){
            int tt=n;
            tt-=4+a[i]+a[j]+a[i+j];
            //if(i==71&&j==71) cout<<tt<<endl;
            if(tt>=2) {
                //cout<<i<<"+"<<j<<"=="<<i+j<<endl;
                if(i!=j) ans+=2;
                ans+=2;
            }else if(tt>=0){ 
                //cout<<i<<"+"<<j<<"="<<i+j<<endl;
                if(i!=j) ans++;
                ans++;
            }
        }
    }
    if(ans>0)cout<<ans;
    else cout<<-1;
    return 0;
}

D.哪一个实验室更厉害呢？

考点：思维、博弈

定位：思维签到

#include<bits/stdc++.h>
using namespace std;

int main()
{
	int n,m;
	cin>>n>>m;
	if(n<=m) cout<<"A!";
	else if(n%(m+1)==0) cout<<"C!";
	else cout<<"A!";
}

E.数字三角回旋镖

考点：模拟、构造

定位：l2模拟签到

p7351.数字回旋三角回旋镖

首先，这道题肯定是利用二维数组打表制作，要知道对应n所需要多少个数字

方法一：

可以用递推的方式获得相应n长度回旋镖需要多少个数字

1 2 3 4 5 6 7 …
1 3 6 10 15 21 28 …

可以很容易得到，s(i)=s(i-1)+i

image

方法二：

​ 对不同长度回旋镖图的观察，可以得到s(n)=(n+1)*n/2;

我们可以把过程分开

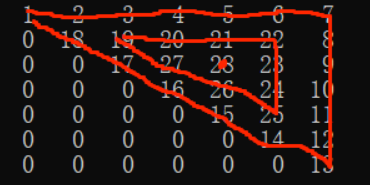
image

很容易发现这是三个类似的三角形环（边长分别为7,4,1）组成，那么我们就可以利用递归（循环）解决。

通过观察可以发现，第一个三角环的起始地址为（1,1），第二个三角环地址为（2,3），第三个为（3,5），那么设第i个三角环的起始地址为（x,y）,所以第（i+1）个的地址就位（x+1,y+2）。

每次三角环的边长都会减少3，所以当边长小于或者等于0时，此时便可以结束。

此为核心代码：

void cz(int x,int y,int flag,int gcc)
{
	int i,j;
	for(i=y;i<n-gcc&&temp!=mx+1;i++)k[x][i]=temp++;
	for(j=x;j<=n-gcc*2&&temp!=mx+1;j++)k[j][i]=temp++;
	for(i--,j-=2;k[j][i]==0&&temp!=mx+1;i--,j--)k[j][i]=temp++;
	if(flag<=0)return;
	cz(x+1,y+2,flag-3,gcc+1);
}
//flag 为当前三角环的边长
//x,y为当前三角环的起始地址
//gcc为当前是第gcc个三角环（从0开始）
//temp为相应打表数字，全局变量，从1开始

我们可以比较容易的利用gcc（第gcc个三角环）来计算出当前三角环的x，y的上限

即，y<n-gcc, x<n-gcc*2

注意输出按照%4d的格式输出

以下为完整代码，可能不是最佳，仅供参考

#include <bits/stdc++.h>
using namespace std;
int n,temp=1,mx;
int k[51][51];
void out()//输出代码
{
	for(int i=1;i<=n;i++)
    {
		for(int j=1;j<=n;j++)
		{
			if(k[i][j]!=0)printf("%4d",k[i][j]);
			else printf("%4d",0);
		}
		cout<<endl;
	}
}
void cz(int x,int y,int flag,int gcc)//核心打表代码
{
	int i,j;
	for(i=y;i<n-gcc&&temp!=mx+1;i++)k[x][i]=temp++;
	for(j=x;j<=n-gcc*2&&temp!=mx+1;j++)k[j][i]=temp++;
	for(i--,j-=2;k[j][i]==0&&temp!=mx+1;i--,j--)k[j][i]=temp++;
	if(flag<=0)return;
	cz(x+1,y+2,flag-3,gcc+1);
}
int main(){
	
    cin>>n;
    memset(k,0,sizeof(k));//二维数组置零
	mx=(n+1)*n/2;//计算一共要用的数字
    cz(1,1,n,0);
	out();
    return 0;
}

F.SPN加密算法

考点：模拟、理解

定位：l3防AK(但是其实很简单)

这个题其实不难，但是难就难在看不懂题面，但其实比赛的时候就会出现这种背景完全不知道的模拟题而且还是纯英文的，其实这个题的思路题面写的很清楚了，甚至伪代码都给了你理解了就能写出来

#include<bits/stdc++.h>
using namespace std;
int K[35],t[35];
//密钥
struct node
{
    int x,y;
} N[5][35];
//S置换以及P置换
int w[35],u[35],v[35];
map <int,int> ma,mb;
int main()
{
    for(int i=0; i<4; ++i)
        for(int j=0; j<16; ++j)
            scanf("%d",&(i%2==0?N[i/2][j].x:N[i/2][j].y));
    for(int i=0;i<16;i++){
    	ma[N[0][i].x]=N[0][i].y;
    	mb[N[1][i].x]=N[1][i].y;
	}
	
//N[0]代表S盒,N[1]代表P盒
    for(int i=0; i<32; ++i)
        scanf("%d",&K[i]);
//密钥K
    for(int i=0; i<16; ++i)
        scanf("%d",&w[i]);
//明文w

// 1.密钥分组
    
    for(int f=0;f<=16;f+=4){
        int cou=0;
        for(int j=f;j<16+f;j++){
            t[cou++]=K[j]; 
        }
        if(f==16)break;

        //求u，w和t异或
        for(int i=0;i<16;i++){
            u[i]=w[i]^t[i];

        }

        // 求v，是s盒输出
        for(int i=0;i<16;i+=4)
        {
            int l=0;
            int m=8;
            for(int j=i;j<i+4;j++){
                // u[i]转成10进制 
                if(u[j])l+=m;
                m/=2;
            }
                      
            // s盒变后
            int x=ma[l];
            int sup=3;

            for(int j=i;j<i+4;j++){
                if((x>>sup)&1)v[j]=1;
                else v[j]=0;
                sup--;
            }
            // cout<<p[n]<<endl;
           
            // 变为2进制，存到v[i];  
        }

        // 求w是vr用p置换得到

        for(int i=0;i<16;i++){
            w[i]=v[mb[i+1]-1];
        }


    }

    for(int i=0;i<16;i++){

        cout<<(v[i]^t[i]);
    }

}

G.永劫将至

考点：字符串

定位：l1签到

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N =1e6+5;
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	string s;
	int a=0,b=0;
	cin>>s;
	for(int i=0;i<s.size();i++){
		if(s[i]>='a'&&s[i]<='z') a+=5;
		else b+=10;
	}
	if(a<b) cout<<"Blend into the darkness！";
	else cout<<"Failure is too heavy for me to bear！"; 


	return 0;
}

H.善良的马同学来给你们出签到题了

考点：构造

定位：l1签到

这道题思路很简单，别搞什么巨多选择分支，太麻烦了，就把24小时制转化为分钟，然后加上时间n之后再转化回去就行了。

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n;
    cin>>n;
    int h,m;
    scanf("%d:%d",&h,&m);
    int fm=(h*60+m+n)%60;
    int fh=(h*60+m+n)/60%24;
    printf("%.2d:%.2d",fh,fm);
    return 0;
}

I.值班

考点：数学，DP

定位：l3防AK

这个题是一个数学题，主要的知识点是组合数学相关的内容，在高中阶段，大家学习过一些组合数学相关的知识。通过对题目进行分析，由于题目说明了每位同学最多只有一个时段不能来实验室值班，且各个时段互不冲突，故每位同学具体在哪个时间段不能在哪个时间段来值班是不会对结果造成影响的。故该问题可以等价为每名同学有一个时段不能来实验室，且时段均不冲突。由此，该问题可以简化成为第i位同学不能在第i个时间段来实验室值班，一共有多少种不同的安排方案。

解决这个问题的方法是采用容斥原理的思想。首先不考虑冲突的情况，即n个元素的全排列。之后，考虑会发生冲突的情况。先考虑时段1，时段1不能够安排第1位同学值班，我们把全排列中，时段1为1的同学的所有情况都去掉，同理，对n个同学都采用这样的操作，这时，由于在统计第1个同学的时候，会同时统计到第2个同学的情况。例如：1 2 3 4 5这种，在统计到时间1和2的时候都会统计到它。于是我们需要利用容斥原理进行一个去重。将这种情况加回来。而一共有多少种重复的方案数呢？通过容斥原理我们知道，同时取到1和2的时候就会重复计算，这时，我们就需要把这些重复的元素去掉。就拿1、2同时选择的情况来说吧，会出现这种情况的可能是(n-2)!。一共有C(n,2)*(n-2)!种情况，这次在去掉的时候，会将同时选择1，2，3的情况在选择1，2和2，3的时候去掉，这时，我们就要把这种情况又加回来，一共是C(n,3) *(n-3)!种情况。以此类推，便可以得到下列的公式：

$$ANS = A(n,n) + (-1)^1C(n,1)*A(n-1,n-1)+(-1)^2C(n,2)*A(n-2,n-2)+(-1)^3C(n,3)*A(n-3,n-3)+ \ldots + (-1)^{n-1}*C(n,n-1)*A(1,1) $$

编程求解该公式即可。

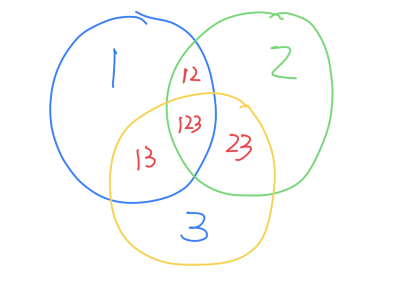
image

上述重复计算的部分示意图。S=1+2+3-12-13-23+123。

代码：

数学做法

#include<bits/stdc++.h>
using namespace std;

int main()
{
	int n,m,i,j;
	long long ans=1;
	cin>>n>>m;
	for (i=1;i<=n;i++)
	{
		ans=ans*i;
	}
	for (i=1;i<=m;i++)
	{
		int s1,s2;
		cin>>s1>>s2;
	}
	int tmp=0;
	for (i=1;i<=m;i++)
	{
		long long sum=1;
		for (j=1;j<=(n-i);j++)
		{
			sum=sum*j;
		}

		for (j=m;j>m-i;j--)
		{
			sum=sum*j;
		}
		for (j=1;j<=i;j++)
		{
			sum=sum/j;
		}
		if (tmp==1)
		{
			ans=ans+sum;
			tmp=0;
		}
		else
		{
			ans=ans-sum;
			tmp=1;
		}
	}
	cout<<ans<<endl;
	return 0;
}

DP做法

#include<iostream>
using namespace std;
typedef long long ll;
const int N = 1e6+5;
ll dp[105][105];
ll a[N],b[N];
int main(){
	ios::sync_with_stdio(false);

	int n,m;
	cin>>n>>m;
	for(int i=0;i<m;i++){
		cin>>a[i]>>b[i];
	}
	dp[0][0]=1;
	for(int i=1;i<=n;i++){
		dp[i][0] = dp[i-1][0] * i;
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			dp[i][j] = dp[i][j-1] - dp[i-1][j-1];
		}
	}
	cout<<dp[n][m];


	return 0;
}

J.贪财的小贼猫

考点：思维，数学

定位：l2较难

#include<iostream>
#include<algorithm>
#include<math.h>
#include<stdlib.h>
using namespace std;
const int N = 1000010;
typedef long long ll;
int n;
ll init[N],c[N];
//首先，最终每个人的金币数量可以计算出来，它等于金币总数除以人数n，
//接下来我们用M表示每人最终拥有的金币数。假设在这个过程中，
//可以设x2表示2号给了1号多少个金币，x3,x4类似。由于是环型，
//x1指的是1号给了4号多少金币。
//对于编号为i的人，初始为Ai，则1号，他最终剩余A1-x1+x2=M。
int main(){
    while(cin>>n){
        ll sum=0;
        for(int i=0;i<n;i++){
            cin>>init[i];
            sum+=init[i];
        }
        ll avg=sum/n;//求出每个人的最终情况 
        c[0]=0;//让c[0]为0,防止c[i-1]出问题 
        for(int i=1;i<n;i++){
            c[i] =c[i-1] + init[i]-avg;//由证明 
        }
        sort(c,c+n);
        ll res = c[n/2],ans=0;//求出中位数 
        for(int i=0;i<n;i++){
            ans = ans+abs(res-c[i]);//由证明 
        }
        cout<<ans<<endl;
    }
    return 0;
}

K.阿拉灯神丁

考点：数学、思维

定位：l2数学思维题

    对任意一个数，如果需要满足余数SiS_{i} = AiA_{i} modmod MM，满足每个SiS_{i}相等,我们可以枚举大于2的数来依次去除每一个数，看他们的余数是否相等，但00<=AiA_{i}<=10910^9，对于大数据依次枚举不符合时间要求。
   若存在一个数MM，满足AiA_{i} modmod MM == Ai+1A_{i+1} modmod MM，同时它们满足 AiA_{i}-Ai−1A_{i-1}可以被M整除。
  
  例如数字11和数字55,有数字22，它们的余数是11，而它们相减为44能被22整除。
  而这个数可以整除所有的**|AiA_{i}-Ai−1A_{i-1}|，问题便转为求各个|AiA_{i}-Ai−1A_{i-1}|之间的一个约数，我们可以用gcd来求得这个是否存在这个数。   
  让 ansans=gcd（|A1A_{1}-A2A_{2}|，|A3A_{3}-A2A_{2}|，...|AiA_{i}-Ai−1A_{i-1}|）。
  
  如果ansans=1，即不存在这个数MM,反之存在数MM可以整除所有的|AiA_{i}-Ai−1A_{i-1}|**，即所有数经过MODMOD MM后相等.

  辗转相除法：

int gcd(int a,int b) {
    int r;
    while(b>0) {
        r=a%b;
        a=b;
        b=r;
    }
    return a;
}

  比如现在要求3232，3636的最大公约数：
   3636 / 2626 = 11...66 (此行除数26作下一行的被除数，余数作为除数)
   2626 / 66 = 44...22 (此行同理)
   66 / 22 = 00 (此处余数为零，意味着最大公约数就是2)
  反复把一个式子中的除数当作被除数去除余数，直到最后余数等于0。
  最大公约数就是最后那个式子的除数，本例就是2。
  
  gcd库函数：

#include <algorithm>
int gcd(int a,int b) {
	return __gcd(a,b);
}

  可以用来求两数的最大公约数。
  
完整代码如下

#include<bits/stdc++.h>
const int N =2e5;
using namespace std;
int a[N]={0};
int gcd(int a,int b) {//辗转相除法
    int r;
    while(b>0) {
        r=a%b;
        a=b;
        b=r;
    }
    return a;
}
int main()
{
	int n,ans=0;
	cin>>n;
	for(int i=1;i<=n;i++)
	cin>>a[i];
	ans=abs(a[2]-a[1]);
	for(int i=3;i<=n;i++)
	{
	//	ans=__gcd(ans,abs（a[i]-a[i-1]));库函数
		ans=gcd(ans,abs(a[i]-a[i-1])); 
	}
	if(ans==1) 
	cout<<"No";
	else
	cout<<"Yes";
	return 0;
}

L.素数求和

考点：数学

定位：l1签到

就大家都知道怎么判断素数，但是这个有两个卡点，第一个就是数据范围很大，所以判断素数的时候要用O(N)O(\sqrt{N})的算法否则就会超时，其次因为数据范围很大所以求和可能会超int，所以应该用long long

#include<stdio.h>
typedef long long ll;
ll check(ll x){
	if(x<2) return 0;
	for(int i=2;i<=x/i;i++){
		if(x%i==0) return 0;
	}
	return 1;
}
int main(){
	ll n,ans=0;
	ll x;
	scanf("%lld",&n);
	for(int i=0;i<n;i++){
		scanf("%lld",&x);
		if(check(x)) ans+=x;
	}
	printf("%lld",ans);

	return 0;
}

0 comments

No comments so far...
610
Accepted
0
Solutions Liked
  1. About
  2. Contact Us
  3. Privacy
  4. Terms of Service
  5. Copyright Complaint
  6. Language
  7. Legacy mode
  8. Theme
  2. 蜀ICP备2021003932号-1
  3. Worker 0, 39ms
  4. Powered by Hydro v4.18.0 Community