1 solutions
-
0
p7351.数字回旋三角回旋镖
首先,这道题肯定是利用二维数组打表制作,要知道对应n所需要多少个数字
方法一:
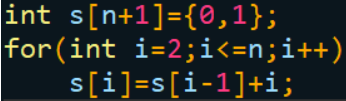
可以用递推的方式获得相应n长度回旋镖需要多少个数字
1 2 3 4 5 6 7 … 1 3 6 10 15 21 28 … 可以很容易得到,s(i)=s(i-1)+i
方法二:
对不同长度回旋镖图的观察,可以得到s(n)=(n+1)*n /2
我们可以把过程分开
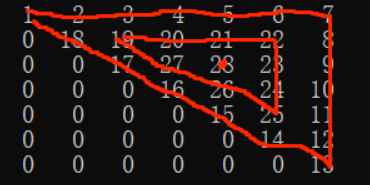
很容易发现这是三个类似的三角形环(边长分别为7,4,1)组成,那么我们就可以利用递归(循环)解决。
通过观察可以发现,第一个三角环的起始地址为(1,1),第二个三角环地址为(2,3),第三个为(3,5),那么设第i个三角环的起始地址为(x,y),所以第(i+1)个的地址就位(x+1,y+2)。
每次三角环的边长都会减少3,所以当边长小于或者等于0时,此时便可以结束。
此为核心代码:
void cz(int x,int y,int flag,int gcc) { int i,j; for(i=y;i<n-gcc&&temp!=mx+1;i++)k[x][i]=temp++; for(j=x;j<=n-gcc*2&&temp!=mx+1;j++)k[j][i]=temp++; for(i--,j-=2;k[j][i]==0&&temp!=mx+1;i--,j--)k[j][i]=temp++; if(flag<=0)return; cz(x+1,y+2,flag-3,gcc+1); } //flag 为当前三角环的边长 //x,y为当前三角环的起始地址 //gcc为当前是第gcc个三角环(从0开始) //temp为相应打表数字,全局变量,从1开始我们可以比较容易的利用gcc(第gcc个三角环)来计算出当前三角环的x,y的上限
即,y<n-gcc, x<n-gcc*2
注意输出按照%4d的格式输出
以下为完整代码,可能不是最佳,仅供参考
#include <bits/stdc++.h> using namespace std; int n,temp=1,mx; int k[51][51]; void out()//输出代码 { for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(k[i][j]!=0)printf("%4d",k[i][j]); else printf("%4d",0); } cout<<endl; } } void cz(int x,int y,int flag,int gcc)//核心打表代码 { int i,j; for(i=y;i<n-gcc&&temp!=mx+1;i++)k[x][i]=temp++; for(j=x;j<=n-gcc*2&&temp!=mx+1;j++)k[j][i]=temp++; for(i--,j-=2;k[j][i]==0&&temp!=mx+1;i--,j--)k[j][i]=temp++; if(flag<=0)return; cz(x+1,y+2,flag-3,gcc+1); } int main(){ cin>>n; memset(k,0,sizeof(k));//二维数组置零 mx=(n+1)*n/2;//计算一共要用的数字 cz(1,1,n,0); out(); return 0; }
Information
- ID
- 6663
- Time
- 1000ms
- Memory
- 256MiB
- Difficulty
- 5
- Tags
- # Submissions
- 63
- Accepted
- 13
- Uploaded By
