$\mathcal {Description}$

$Peano$ 曲线是一条平面内的曲线。 下图给出曲线的 $1$ 阶情形，它是从左下角出发经过一个 $3 × 3$ 的方格中的每一个格子，最终到达右上的一条线。

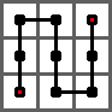
给出 $Peano$ 曲线的 $2$ 阶情形是经过一个 $3^2 × 3^2$ 的方格中的每一个格子的一条曲线。它是将 $1$ 阶曲线的每个方格由 $1$ 阶曲线替换而成。

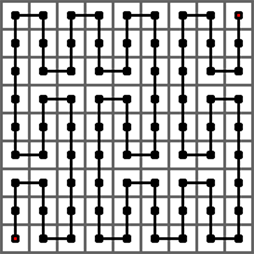
下图给出了 $Peano$ 曲线的 $3$ 阶情形，它是经过一个 $3^3 × 3^3$ 的方格中的每一 个格子的一条曲线。它是将 $2$ 阶曲线的每个方格由 $1$ 阶曲线替换而成。

我们将这些格子放到坐标系中，对于 $k$ 阶 $Peano$ 曲线，左下角的坐标是(0,0)，右上角坐标是 (3^k − 1,3^k − 1)，右下角坐标是 (3^k − 1,0)，左上角坐标是(0,3^k − 1)。 $Peano$ 曲线总是从左下角开始出发，最终到达右上角。 给定 $k$ 阶 $Peano$曲线上的两个点的坐标，请问这两个点之间，如果沿着 $Peano$ 曲线走，距离是多少？

$\mathcal {Format}$

$\mathcal {Input}$

输入的第一行包含一个正整数 $k$，Peano曲线的阶数。 第二行包含两个整数 $x_1 , y_1$ ，表示第一个点的坐标。 第三行包含两个整数 $x_2 , y_2$ ，表示第二个点的坐标。

$\mathcal {Output}$

输出一个整数，表示给定的两个点之间的距离。

$\mathcal {Samples}$

1
0 0
2 2

8

2
0 2
0 3

13

$\mathcal{DataScale}$

对于 $30$ % 的评测用例，$0 ≤ k ≤ 10$。

对于 $50$ % 的评测用例，$0 ≤ k ≤ 20$。

对于所有评测用例，$0 ≤ k ≤ 100$, $0 ≤ x_1 ,y_1 , x_2 ,y_2 < 3^k$ , $x_1 ,y_1 , x_2 ,y_2 ≤ 10^{18}$ 。 数据保证答案不超过 $10^{18}$ 。

$\mathcal {Limitation}$

$1$s, $1024$KiB for each test case.